Konvolusi merupakan konsep matematika yang sering digunakan untuk aplikasi pemrosesan image (gambar) atau sinyal.
Dalam pengolahan gambar, konvolusi digunakan sebagai filter untuk mengubah karakteristik gambar, mempertajam batas gambar, mengaburkan gambar atau menghapus noise pada gambar.
Pada pemrosesan sinyal, konvolusi adalah metode yang menggambarkan bagaimana setiap sistem linear h[n] mempengaruhi input x[n] untuk menghasilkan output y[n] yang sesuai. Konvolusi juga dapat digunakan untuk menekan bagian yang tidak diinginkan dari sebuah sinyal atau untuk memisahkan sinyal menjadi bagian-bagian yang berbeda atau lebih dikenal dengan proses filtering. Lebih khusus, output y[n] dikatakan konvolusi dari sinyal input x[n] dengan fungsi sistem respon karateristik h[n] dan ditulis menjadi y [n] = h [n] * x [n] .
Secara umum, dua fungsi dari continuous convolution, bisa didapatkan dengan h[x] dan g [x], dapat didefinisikan oleh integral konvolusi.
Dalam pengolahan gambar, konvolusi digunakan sebagai filter untuk mengubah karakteristik gambar, mempertajam batas gambar, mengaburkan gambar atau menghapus noise pada gambar.
Pada pemrosesan sinyal, konvolusi adalah metode yang menggambarkan bagaimana setiap sistem linear h[n] mempengaruhi input x[n] untuk menghasilkan output y[n] yang sesuai. Konvolusi juga dapat digunakan untuk menekan bagian yang tidak diinginkan dari sebuah sinyal atau untuk memisahkan sinyal menjadi bagian-bagian yang berbeda atau lebih dikenal dengan proses filtering. Lebih khusus, output y[n] dikatakan konvolusi dari sinyal input x[n] dengan fungsi sistem respon karateristik h[n] dan ditulis menjadi y [n] = h [n] * x [n] .
Secara umum, dua fungsi dari continuous convolution, bisa didapatkan dengan h[x] dan g [x], dapat didefinisikan oleh integral konvolusi.
Hal ini dapat dengan mudah ditunjukkan bahwa h(x) * g(x) = g(x) * h(x), yang berarti bahwa operasi konvolusi adalah komutatif, yang berarti bahwa dapat juga ditulis menjadi :
Menggunakan rectangle method, integral konvolusi di atas dapat didekati dengan :
Dimana Δα hanya scaling factor lebih dikenal sebagai interval sampling. Secara umum, integral konvolusi ini dapat didekati dengan hasil penjumlahan sepasang nilai diskrit dan memiliki hasil akhir yang dikalikan dengan faktor penskalaan.
Dengan demikian definisinya adalah, jika x[n] adalah sinyal digital N-titik yang berjalan dari 0 sampai N-1, dan h[n] adalah sinyal digital M-titik yang berjalan dari 0 sampai M-1, konvolusi dari dua sinyal y[ n] = x[n] * h[n] adalah sebuah sinyal N+M-1 yang berjalan dari 0 sampai N+M-2.
Source code di bawah ini mengilustrasikan bagaimana kedua metode perhitungan konvolusi diskrit dari dua sinyal dapat diimplementasikan dalam C # :


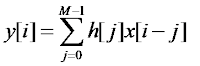




No comments:
Post a Comment